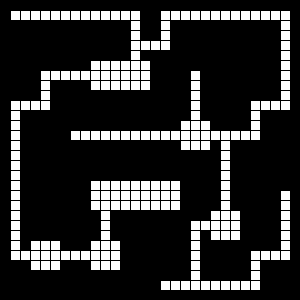
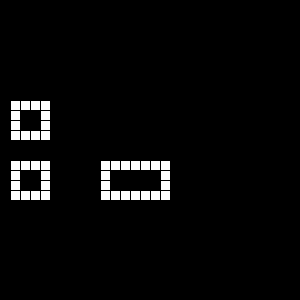Maze Walk Through
It's a'mazing I call this a walk through.

First Things First
- Don't expect much code.
- I woke up with time on my hands, realized I didn't feel like filling it by working on this project, so time to put it on ice.
- Last time, I waited six months between my last coding spree and the web debriefing. I'm not going to do that again.
Getting Something on the Screen
Pretty much, nearly always, my first step.
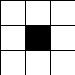
Each 'cell' in the mazes that follow are represented by a 3x3 gridded image, something like the above (pictures above, comments below).

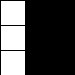
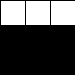
Here, we have six of the first tiles grouped together (3x2).
Below and everything else on the page consists of 10x10 cell 'mazes' in 300x300px image form. Remember, each cell is comprised of a 3x3 tile. So, the gridded images are a 30x30 grid mesh. And believe it or not, that little bit of complication probably saved me a whole heck of a lot of more complications further on, so well worth it in my opinion.
In the above, each square gets a random passage segment (white) radiating from the centre of the cell in one random direction. In each successive image, an additional random passage segment is added, which may be a duplicate of one already added. Given enough iterations, this would terminate in a solid white 30x30 mesh grid.
For the most, this is a proof of concept. 'See's,' I's says to myself, 'All's you's has to do is get that white space looking right and you've got yourself a dungeon, maze, or's whatevers.'
And going back and applying a 'clean up' function to the above (something I only developed near the end of this project), and I do, indeed, get something that looks mazish, dungeonish, or whateverish (pretty much right at the start).
So, really, I could have been finished almost before I began if I only knew what I was doing...
Stack Mazes
Everything is easy, once you know the secret.
This is the simplest algorithm that I know for making a maze that covers the entire board (visits every square, i.e. makes a connected graph).
- Choose a cell at random, place it on the stack.
- If cell on top of stack has unvisited neighbours, connect to one neighbour at random, and place the neighbour on the top of the stack, repeating ad infinitum.
- Else if cell on top of stack has no unvisited neighbours, pop cell, and look at next cell in the stack.
Probably not the clearest. But, hey! That's why there are other websites on the Internet. But it's really not that hard. Though, to be fair, it was the first time I had need of a stack for... pretty much, anything.
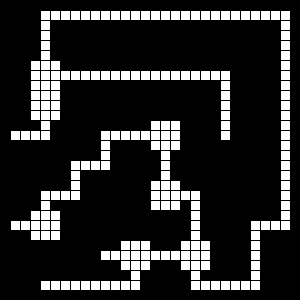
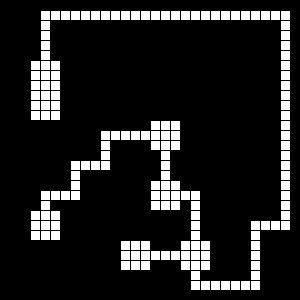
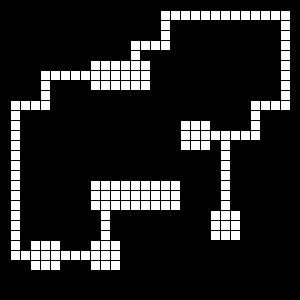
Stack maze, the 'rooms' are how I implemented four-way intersections. Notice how all the 'rooms' are connected on four sides.
Stack maze, spurs removed (single exit paths), dead ends deleted (pathways not connecting rooms deleted).
Huh! What do you know. All these look pretty similar. But that's more because they were 'selected' from the possibilities by yours truly.
So, hopefully, these look a little different. Or if not, personally, I was quite pleased when adding the lines back in took exactly two lines of code, basically passing **kwargs through (oh, I use Python pretty much exclusively, so if that makes no sense, um, Python).
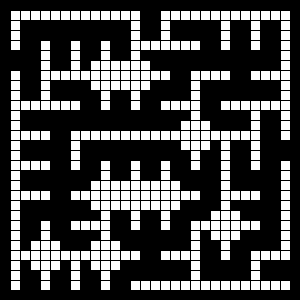
This is basically the same thing, only on a larger scale, because, you know, 'Does it scale?'
Test Pattern Madness
When in doubt, put something. anything, to the screen, even if it's just some static image; and then, jiggle it a little. You know, poke at it.
Actually, I think what really happened is that I didn't know what to do next, so, um, yeah Test Pattern Madness.
Pretty basic stuff, made with for/next loops.
Vertical then horizontal, with each being the raw pattern after the connect maze algorithm was applied; and then, cleaning up the spurs and dead ends.
To 'connect' these, I used a new algorithm that I called connected. Clever, huh? But what is even more clever, is leaving the explanation as to what that means for the next section. And of course, by explain, I mean completely gloss over. But hey, you get what you pay for.

Connected
It's all connected, dude!
- ✯ Add a few rooms at random
- ✯ Run the stack maze algorithm.
- ✯ Clean up spurs and dead ends.
- ✯ Remove rooms unconnected to main maze.
- ✯ Easy Peasy.
From left to right, a stack maze using a bunch of random 'rooms' (four way intersections) as random seeds, then killing spurs, finally removing hanging rooms.
I considered two cells connected if each cell had a passageway leading to the other cell. In other set ups, a one directional check might be sufficient, but my 'rooms' are four-way intersections, so I had to check in both directions (otherwise, my 'rooms' would connect to all four sides all the time).
Then, by checking all cells that a cell connected to, I assembled a list of connected cells. And if that list wasn't long enough, all cells in the list got blacked out (or conversely, if it was long enough, all cells were left alone and removed from the 'to check' list).
Not rocket science, but I'd wager that stacks are the way to go:
Connected? I think not,
in more ways than one...
Connecting Code
Just enough code to be less than useless...
def connected_list(self, cell):
'''Returns list of all cells cell is connected to.
Note: a cell is always connected to itself.'''
to_visit = [cell]
visited = set()
while to_visit:
current = to_visit.pop()
visited.add(current)
for wall in 'NSEW':
#1 is a passage leading out, 0 is a wall
if 1 == getattr(current, wall):
cell_next_door = self.neighbor_cell(current, wall)
#cell_next_door must have a passage back (i.e. a 1)
if 1 == getattr(cell_next_door, opposite_wall(wall)):
if cell_next_door not in visited:
to_visit.append(cell_next_door)
return visited
def kill_small_areas(self, cut_off=10):
'''Kill areas that link to less than cut_off value.'''
#no need process all black (0 value cells)
cells = [cell for cell in self.cells if not cell.is_all_black()]
#cells is the stack
while cells:
#get a list of connecgted cells and process
connected = self.connected_list(cells[0])
for c in connected:
#set to black if a small area
if len(connected) < 10:
c.set_solid(val=0)
#either way, this cell (c) has been processed
cells.remove(c)
Post Mortem
You know, what did I learn?
- ✨ Well, first, I'll figured out how to do star lists. So, yippie!
- ✩ Second, stacks (see the above example).
- ✪ Third, lists of objects (probably should explain that more, so at least one more section, lucky you).
- ✫ And probably finally, in the interest of staying interested, I should pull the plug faster.
- ✯ So, you know, no more list items, here, of what I learned. Still, that star thing is pretty cool.
List of Objects as an Object
You know, because in Python, everything is an Object.
class Cell():
'''Individual cell (space) in the maze (grid).'''
def __init__(self, row, col):
'''Each row/col pair together form an ID and must be unique.
N, S, E, W are walls and initialized to zero,
which means a wall is present
0 = black, 0 = wall
1 = white, 1 = open space.'''
self.row = row
self.col = col
self.N = 0
self.S = 0
self.E = 0
self.W = 0
class Maze():
'''Cell holding structure that forms a maze/grid.'''
def __init__(self, rows=10, cols=10, lines=True):
'''Maze/Grid holding structure.
rows: number of cell units tall
cells will ultimately equal tiles in checkered
cols: number of cell units wide
lines: if true, white areas will be drawn with grids
used as a pass-through to checkered_tiles.lines
'''
self.rows = rows
self.cols = cols
self.lines = lines
self.cells = []
self.init_cells(rows, cols)
def init_cells(self, rows, cols):
'''Rebuilds cells list, zeroing out all cells in process.'''
self.cells = []
for row in range(rows):
for col in range(cols):
self.cells.append(Cell(row, col))
I haven't got the slighted idea how helpful that is. But in short, the central part of a Maze object is a list of Cell objects. That is to say, the purpose of the Maze Class is to provide a structure that holds together a grouping (i.e. a list) of Cells.
And although I do not know what the Design Pattern for this is called, recently it has become very important to me, making the organization of complex structures all the easier.
And that, my friends, is all I have to say about that.
The Infamous Home Page
paufler.net@gmail.com
Terms of Service
✤ ✥ ✦ ✧ ✨ ✩ ✪ ✫ ✬ ✭
© Copyright 2016 Brett Paufler ©
✮ ✯ ✰ ✱ ✲ ✳ ✴ ✵ ✶ ✷